入出力
RDE からプログラムをファイルに保存する、RDE 上でファイルからプログラムを読み込む:
実際にやってみる。
コンソール入出力:
| 関数名 |
意味 |
備考 |
| gets | コンソールからの文字列の入力 |
|
| gets.to_i | コンソールからの整数の入力 |
本当は gets が返す文字列へ to_i メソッドを送っている |
| gets.to_f | コンソールからの浮動小数点数の入力 |
本当は gets が返す文字列へ to_f メソッドを送っている |
| puts(obj) | コンソールへの出力 |
()は省略可能、最後に改行を出力 |
| p(obj1,...) |
コンソールへの出力(どちらかというとデバッグ用?) |
()は省略可能 |
| print(arg1,...) |
コンソールへの出力 |
()は省略可能 |
| printf(format,arg,...) |
コンソールへのフォーマット出力 |
()は省略可能、フォーマットの詳細は
オンラインマニュアルを参照
|
演習:
s = "いろはにほへと"
i = 12345
f = 3.1415
printf("s は %s で i は %d で f は %f です。\n", s, i, f)
第05回の補足
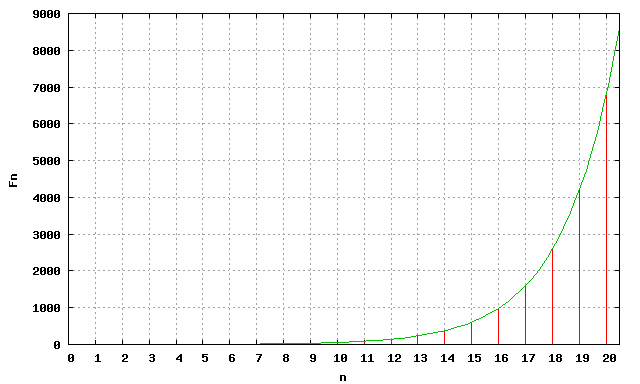
問5(発展課題): n を大きくしていくと計算時間はどうなるでしょうか?
まず Fn の一般形を求める。
二次方程式 z2-z-1 = 0 の(異なる)2つの解を各々
- α = (1+√5)/2 = 1.6180 ... ← いわゆる黄金比
- β = (1-√5)/2 = 1-α = -0.6180 ...
とおくと
- (α0 - β0)/√5 = (1-1)/√5 = 0
- (α1 - β1)/√5 = (α-β)/√5 = √5 / √5 = 1
-
(αn - βn)/√5
-(αn-1 - βn-1)/√5
-(αn-2 - βn-2)/√5
= (αn-2(α2-α-1) - βn-2(β2-β-1))/√5
= (αn-2 0 - βn-2 0) / √5
= 0
という関係が成立する。したがって任意の n について
Fn = (αn - βn)/√5
と表現できる。
より一般的な解法はたぶん線形代数の講義あたりで学習している(あるいはする)
と思いますが、たとえば番号を1個ずらす線型写像を考えてそれを表現する行列の
冪乗の一般形を求める問題に帰着させるという方法があります。
いま考えている Fibonacci 数列の場合はその行列が
ですから R の特性方程式 z
2-z-1 = 0 が現れてくると。
また初期値 F
0 と F
1 を変更した場合も
α
n とβ
n の線形結合で F
n が表現されることも
わかります。
def fib1(n)
if n==0
return 0
elsif n==1
return 1
else
return fib1(n-1) + fib1(n-2)
end
end
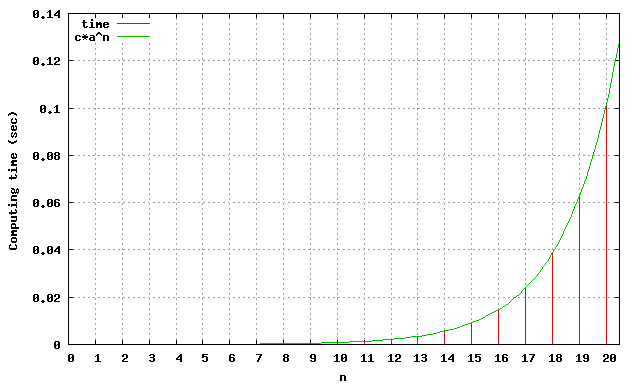
について fib1(n) を計算するために必要な時間を Tn とする。
大雑把に考えて Tn = Tn-1 + Tn-2
であるから、Tn は Fibinacci 数列 Fn と同様の増加傾向を辿ることになり、ほぼ αn に比例することとなる。
参考: 上図は実測値である(αn に対する比例定数 c は約 1/150000)。
問9(発展課題): fib2(n) の計算には n 回ループを廻す必要がありますが、もうちょっと
頑張ると log(n) 回程度のループで済ますことが可能です。そのような関数
fib3(n) を定義してみましょう。
と定義したとき
| ( |
Fn+1 |
) |
= |
( |
1 | 1 |
) ( |
Fn |
) |
| Fn |
1 | 0 |
Fn-1 |
すなわち
Vn = R Vn-1
となる。よって
| ( |
Fn+1 |
) |
= |
( |
1 | 1 |
) |
n
|
( |
F1 |
) |
| Fn |
1 | 0 |
F0 |
すなわち
Vn = Rn V0
が成立する。ここで
さて R は対称行列であるから Rn も対称行列となる。そこで
と an, bn, cn (n > 0)
を定義すると
a1 = 1,
b1 = 1,
c1 = 0
である。
さて次の式
| ( |
a2n | b2n |
) |
= R2n = |
Rn Rn = |
( |
an | bn |
)( |
an | bn |
) |
= |
( |
anan+bnbn |
|
bn(an+cn) |
) |
| b2n | c2n |
bn |
cn |
bn |
cn |
bn(an+cn) |
|
bnbn+cncn |
を考慮すると
R, R2, R4, R8, ...
という R2i (i=0,1,2...)の列が次々と計算できる。
したがって n の2進数表記を nk nk-1 ... n0
(各 ni は 0 か 1 の値をとる)とすれば
Rn
= R
nk2k
+ nk-12k-1
+ ...
+ n020
=
R nk2k
R nk-12k-1
…
R n020
Vn =
R nk2k
R nk-12k-1
…
R n020
V0
となる。したがって
R2i (i=0,1,2...k)を次々と計算し
ni が 1 だったら R2i を
V0 に対して乗ずる、という操作を k 回おこなうと
Vn (すなわち Fn)が求まることになる。
この「アルゴリズム」を ruby でプログラムしたものが fib3 である。
# n 回ループを廻るアルゴリズム
def fib2(n)
a = 1; b = 0
while n > 0
t = a; a += b; b = t; n -= 1
end
return b
end
# 約 log(n) 回ループを廻るアルゴリズム
def fib3(n)
m = n # n をそのまま使ってよいが説明の便宜上 m という新しい変数を使う
i = 0 # 不要な変数だが説明の便宜上用意してある
x=1; y=0 # 初期値は V(0) の要素 F(1) と F(0)
a=1; b=1; c=0 # R^(2^i) の要素 a,b,c が記録される変数
while m > 0 # for i in 1 .. k と同じ
if m % 2 == 1 # m の2進表記の0桁目(最下位ビット)が 1 である
# つまり n の2進表記のi桁目が 1 である
x2 = x; y2 = y
x = a*x2 + b*y2
y = b*x2 + c*y2
end
i += 1 # 着目する桁を1つ進める
m /= 2 # 余りを無視し 2 で割った値で m を置き換える(右シフトする)
# R^(2^i) の計算
aa = a*a; bb = b*b; cc = c*c; a_c = a+c
a = aa + bb; b *= a_c; c = bb + cc
end
# while ループ終了時には V(n) が計算できている
return y
end
for i in 0 .. 15
# i に対して幅2桁で10進表記(幅4桁で2進表記)
# fib2(i) の値を幅4桁で10進表記
# fib3(i) の値を幅4桁で10進表記
printf("%2d(%4b) %4d %4d\n", i, i, fib2(i), fib3(i))
end